MODELO EOQ CON DEMANDA PROBABILÍSTICA.

Con el pasar del tiempo se ha tratado de adaptar el modelo determinístico de cantidad económica  de pedido EOQ para que refleje la naturaleza probabilista de la demanda, usando una aproximación que sobrepone una existencia constante de reserva sobre el nivel de inventario. El tamaño de la reserva (punto de reorden) se determina de tal modo que la probabilidad de que se agote la existencia durante el tiempo de entrega (el periodo entre la colocación de la orden y la recepción del pedido) no sea mayor que un valor especificado.

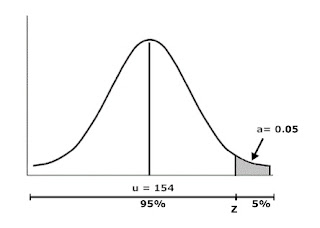
La hipótesis principal de este modelo es que la demanda durante el tiempo de entrega, tiene una distribución normal, con media μ y desviación estándar σ. (μ se define como la demanda promedio durante el tiempo de entrega y σ es la desviación estándar de la demanda durante este mismo periodo).

El valor promedio de  la demanda, la cual podemos ver ubicada en el punto medio de la curva de distribución normal, nos da a saber que existe  una probabilidad de que  en el 50% de las veces nuestro inventario no podrá satisfacer los requerimientos del mercado. Por tal razón al implementar este sistema de inventario, se debe establecer en primera instancia un porcentaje tolerable de error (α= probabilidad  máxima admisible de que se agote la reserva durante el tiempo de entrega), en otras palabras un número de veces en el que se es permitido que la demanda supere nuestras reservas y no se pueda satisfacer con las exigencias del mercado.

Dos números críticos dentro de este sistema son, el  punto de reorden (R)  y la cantidad a pedir (Q). La política de inventario se puede resumir en estas dos variables, de la siguiente manera: Siempre que el nivel de inventario de un producto baje a R unidades, se coloca una orden de Q unidades para reabastecer el inventario. Estas dos variables se ven condicionadas por el tiempo de entrega (L), periodo en el cual la fluctuación de la demanda determinará el punto mínimo de  unidades a mantener en inventario. Q se determinará como se venía haciendo en el modelo básico de EOQ

En resumen las variables de este modelo son : 

L= tiempo  den entrega entre la colocación de la orden y la recepción del pedido.

μL = Demanda promedio durante el tiempo de entrega.

σL = Desviación estándar de la demanda durante el tiempo de entrega

R = Punto de reorden (tamaño de la existencia de reserva).

α= Probabilidad máxima admisible de que se agote la existencia durante el tiempo de entrega. 

La demanda durante el tiempo de entrega L se suele describir con una función de densidad de probabilidades por unidad de tiempo (es decir por día o por semana), a partir de la que se puede determinar la distribución de la demanda durante L. Dado que la demanda por unidad de tiempo es normal, con media D y desviación estándar σ, la media μL y la desviación estándar σL de la demanda, durante el tiempo de entrega L, se calculan como sigue: 

  EL punto de reorden entonces lo definimos como:

En donde el valor de Z se encuentra en las tablas de distribución normal y toma el valor de Z = 1-α

Procedamos mediante un ejemplo a emplear lo anteriormente explicado.

Como tenemos que Z = 1-0.05 = 0.95 procedemos a encontrar este valor en la tabla de distribución normal

Interpolando encontramos que el valor de Z es 1.645 por lo cual tenemos que nuestro punto de reorden es igual a

R= cuando en el inventario hayan 195 unidades se procederá a emitir una orden de pedido de 400 unidades. 

REGLAS FUNDAMENTALES DE LA ADMINISTRACIÓN DE INVENTARIOS.

1.   Toda entrada y salida de inventario debe estar debidamente documentada.

2.   Todo ítem debe estar debidamente codificado (Ubicación y Localización).

3.   En cuanto sea posible, todos los ítems deben estar guardados en el mismo lugar.

4.   Nunca, jamás, recibir comisiones de los proveedores (ni finas atenciones).

5.   En cuanto sea posible, el lugar físico en conde se realiza la recepción de materiales debe ser diferente al lugar donde se entregan y sale la mercancía.

6.   Los ítems de mayor peso deben estar organizados desde el de menor peso al de mayor peso (de arriba hacia abajo).

7.  Ningún miembro del equipo del almacén se puede ir hasta que no haya un conteo físico de los ítems que tuvieron movimiento ese día.

8.  Se deben contar los mismos ítems por 3 auditores diferentes y se consignan aquellos que tengan al menos 2 resultados iguales.

9.   En el punto más lejano del inventario debe haber un extintor.

10. Los reportes de Inventario deben estar, como máximo, terminados 3 días hábiles después del cierre del ciclo contable.

MODELO EOQ CON DESCUENTOS CON CANTIDADES

En los modelos anteriores se hizo la suposición que el costo por unidad de un artículo es el mismo sin importar las cantidades en el lote. De hecho, esta suposición da como resultado que las soluciones óptimas sean independientes del costo por unidad. En el modelo EOQ con descuento por cantidad esa suposición es sustituida  por la siguiente:

El costo unitario de un artículo depende ahora, de la cantidad del lote. En particular, se proporciona un incentivo para colocar una orden grande al cambiar el costo unitario de cantidades pequeñas por un costo unitario menor en los lotes grandes y quizá un costo unitario todavía más pequeño para lotes aún más grandes.

Las suposiciones restantes son iguales a las del modelo EOQ básico. 

Para ilustrar mejor este hecho procederemos mediante un ejemplo.

Ejemplo

Una empresa local de contaduría en Guatemala pide cajas de 10 disquetes a un almacén en la ciudad. El precio por caja que cobra el almacén depende del número de cajas que se le compren. La empresa de contadores utiliza 10000 disquetes por año, el costo de hacer un pedido es de $ 100 dólares. El único costo de almacenamiento es el costo de oportunidad de capital, que se supone 20% por año.

Cada vez que se hace un pedido de disquetes, ¿Cuántas cajas se deben pedir?¿Cuál es el costo anual total para cumplir con la demanda de disquetes por parte de la empresa de contadores?

Solución

Cp =  $ 100 (anual)

d= (10000 disquetes/año)/(10 disquetes/caja)=1000 Cajas/año

Cmi = 20%Cu

En primera instancia procedemos al cálculo de las respectivas cantidades a pedir de acuerdo al costo unitario ofrecido en cada opción.

Opción 1

El valor obtenido en la primera opción, de la cantidad óptima a pedir  es de 141 cajas. Como podemos observar éste número  sobrepasa el rango establecido en la oferta realizada por parte del productor, por tal razón tomamos el valor máximo de esta opción es decir 99 unidades es la cantidad óptima a pedir en esta opción. 

Opción 2

El valor obtenido de la cantidad óptima a pedir en la segunda opción es de 143 cajas, como podemos observar este número cae dentro del rango establecido por el oferente en esta alternativa. Así que en este punto se establece que 143 cajas es la cantidad óptima a pedir en esta opción.

Opción 3

El valor obtenido de la cantidad óptima a pedir en esta opción es de 144 cajas, como podemos observar es menor al rango establecido por parte del oferente por tal razón con el fin de  aprovechar el descuento ofrecido, se toma como cantidad óptima a pedir el mínimo valor  de esta alternativa que sería 300 cajas.

Los resultados obtenidos en cada opción fueron

Como podemos observar de las tres opciones tan solo la segunda cae dentro del rango establecido por  el oferente, más aun así este no es un criterio suficiente para determinar cuál será la cantidad óptima a pedir. Para tal efecto procedemos al cálculo del costo total anual en el que se incurre con cada opción. 

Como podemos observar la opción 3 es la que nos ofrece los menores costos anuales, y por tal razón se muestra como la mejor alternativa. La cantidad óptima a pedir es de 300 cajas por pedido, generando costos anuales de $ 50288.33

Cuando existen descuentos la cantidad óptima a pedir esta sujeta o depende del costo anual que genere, y será ese el criterio para poder elegir una opción.